Нахождение оптимального уровня секьюритизации

Итак, мы имеем целевую функцию инвестора, которую нужно максимизировать, а также три вида ограничений, рассмотренных выше:

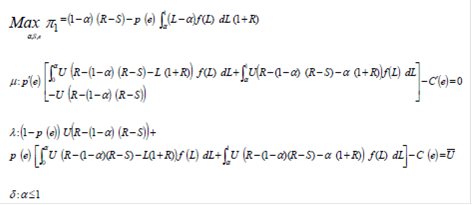
Отстутствие морального риска:

Прежде всего,мы полагаем что (условие отсутствия морального риска), и e=e**.Инвестор выбирает уровень усилия и устанавливает его на уровне e**,используя стратегию «take it or leave it».

Продифференцируем по S,функцию Лагранжа,полученную из целевой функции и данных ограничений и приравняем к 0,после чего домножим обе части на :

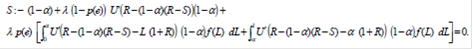
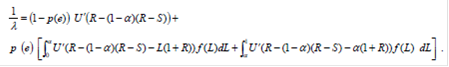
Аналогичные преобразования проделываем с продифференцированной функцией Лагранжа по a, пропустим несколько ненужных математических выкладок для анализа и получим следующее:

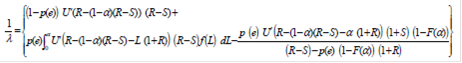
Приравняем полученые функции (мы это можем сделать, так как они обе равны значению ) и найдем, что решением данного уравнения:

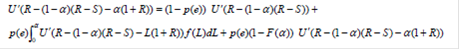
Является значение a=0.Мы также можем убедиться,что R>S в оптимуме.

Инвестор использует свои возможности,чтобы извлечь рисковую премию у несклонного к риску банка.В условиях нейтральности к риску,(R-S) будет равно ожидаемым потерям.

ü В условиях морального риска:

Теперь мы полагеам,что занчение вследствие того, что угроза морального риска ощущаема участниками. Продифференцируем по S и после упрощения получим:

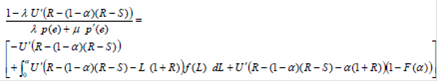
Аналогичные вычисления проводим,дифференцируя по a, и после упрощения получим:

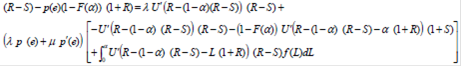
Эти два условия первого порядка можно записать в виде:

Где U’(R-(1-a)(R-S)-a(1+R))=U’(3)

Мы рассмотрим 2 ситуации:

.Положим и получим следующее неравенство,которое будет выполняться в случае,когда a будет меньше или равно нулю.Это связано с тем,что U’ убывает по уровню благосостояния w.Так как a не может быть меньше нуля,мы вновь сталкиваемся со случаем совершенной секьюритизации(a=0).

Подставив a=0 неравенство,получим:

Что в свою очередь является противоречием, так как F(0)=0.И мы отвергаем данный случай.

.Положим :

Так как U’ убывает по уровню благосостояния w, значени a должно быть больше или равно нулю ,чтобы решить данное неравенство.Это означает, что совершенная секьюритизация не является оптимальным решением,и должно иметь место некое удержание траншей в условиях морального риска.Оптимальное решение a*>0 означает, что:потери инвестора = a*>0 , то есть они имеют положительное значение.

Поэтому: Потери инвестора=L-a*>=0;

Если L<a*:Потери инвестора=0;

Если L>=a*:Потери инвестора=L-a*.

Наконец,мы понимаем,что полное удерживание также может быть оптимальным решением задачи.

Заключение

В последнее время рынок секьюритизации активов развивается стремительными темпами. А значит рассмотренная проблема приобретает с каждым днём всё большую актуальность, в частности, особенно для коммерческих банков, имеющих значительные портфели однородных кредитов, лизинговых компаний, фондов недвижимости и девелоперов. В данной работе была рассмотрена методика для получения оптимального распределения рисков между продавцами и покупателями данных «продуктов секьюритизации» в условиях морального риска. Доказано, что оптимальный контракт должен содержать частичное удержание в присутствии морального риска.Соответственно оптимальное количество удержания может быть рассчитано с использованием данной модели с различными значениями параметров.

Другое по теме

Роль инвестиционной деятельности в развитии предприятия ООО Симплекс
Результаты в любой сфере бизнеса зависят от наличия и эффективности использования от инвестиционной деятельности предприятия. Поэтому забота об инвестициях является отправным моментом и конечным результатом деятельности любого субъекта хозяйствования. В условиях рыночной экономики эти вопросы ...